Venn Diagrams
Venn Diagrams:- Earlier we have discussed two
methods to represent a set (i) Roster form and (ii) Set Builder form. The third method to represent a set is by diagrams or pictures called Venn-diagram (also called Venn-Euler diagrams)
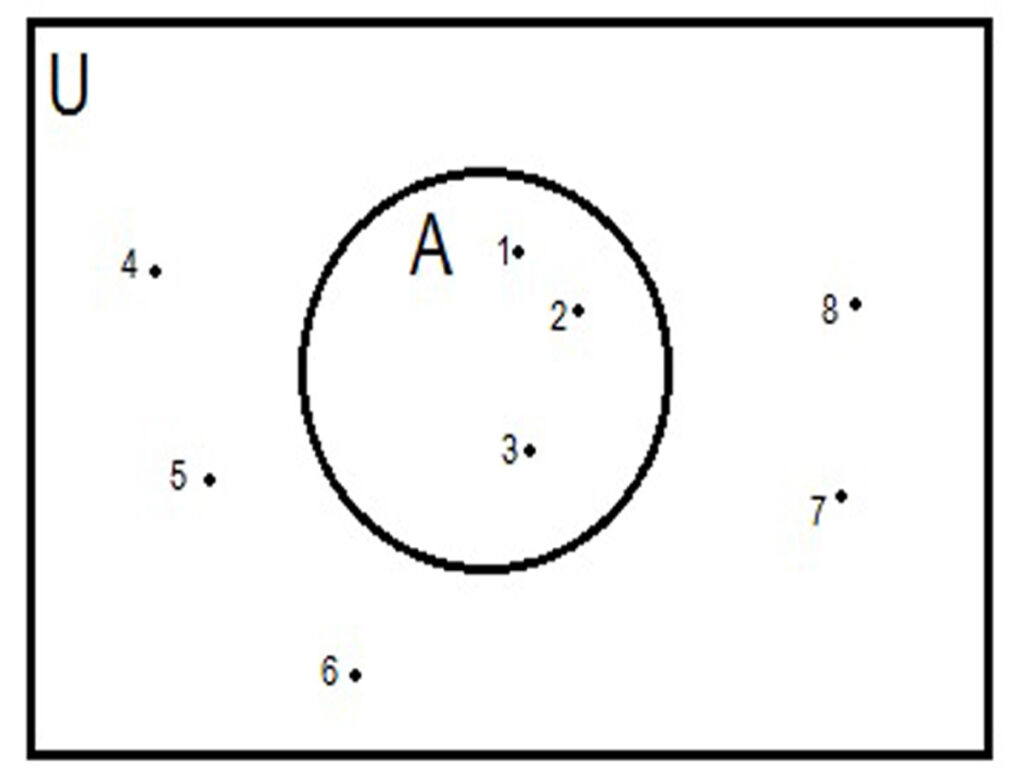
In this method universal set is represented by a rectangle and other sets are represented by
circles (or closed curves)
Let us understand it with the help of examples:-
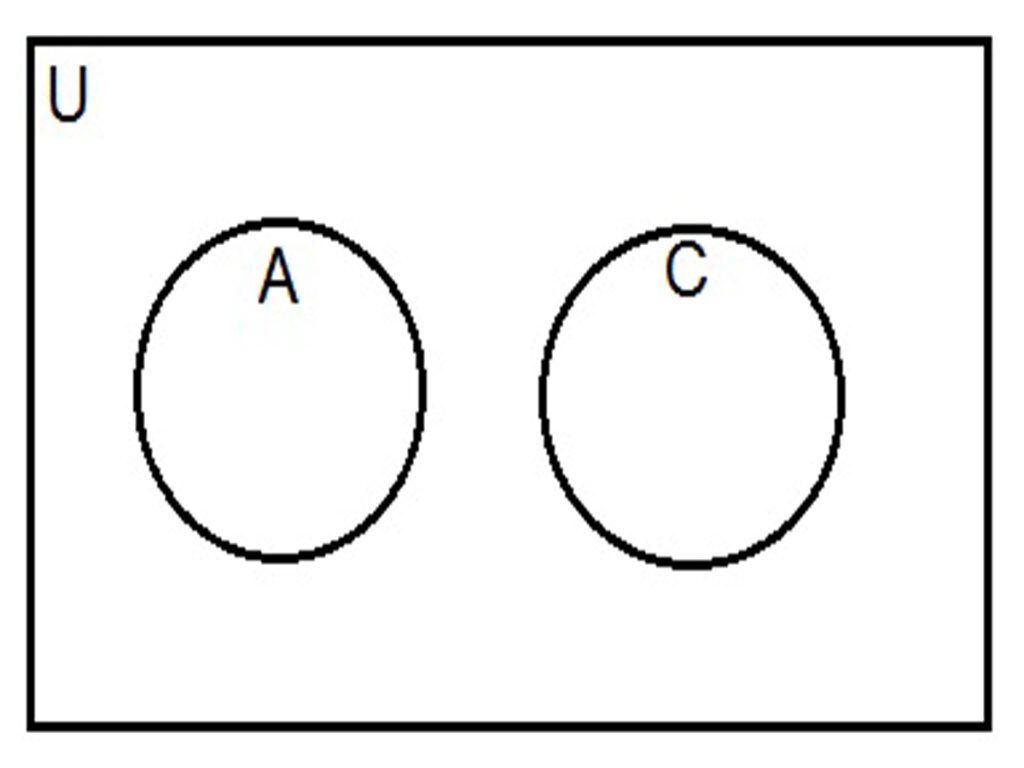
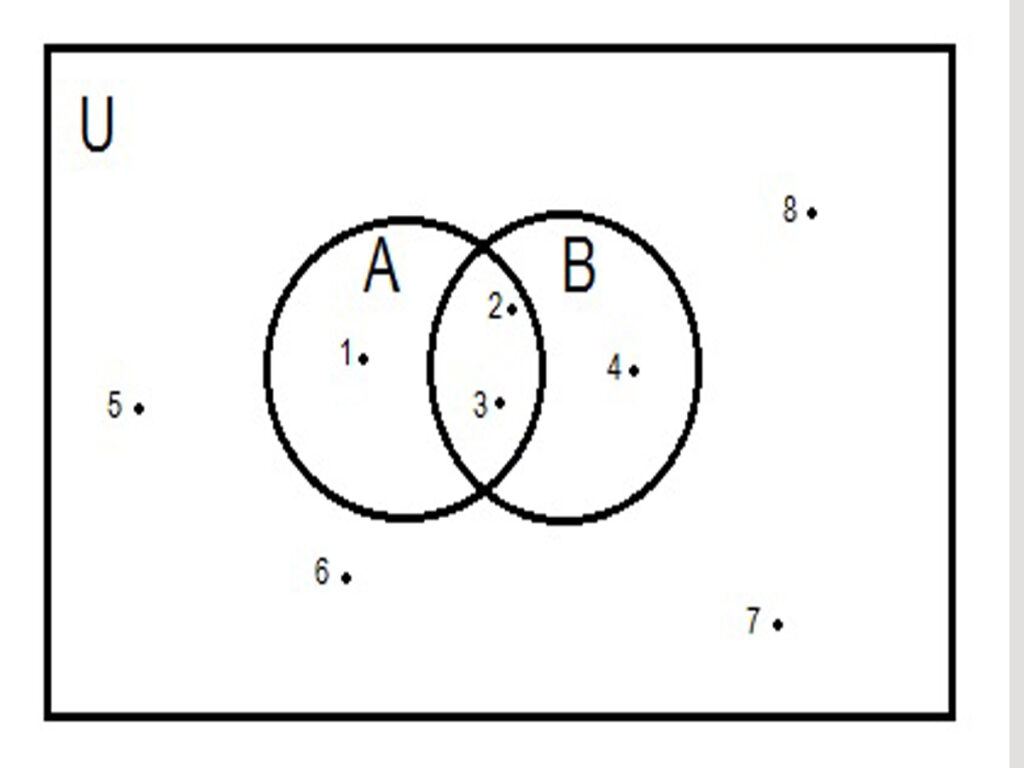
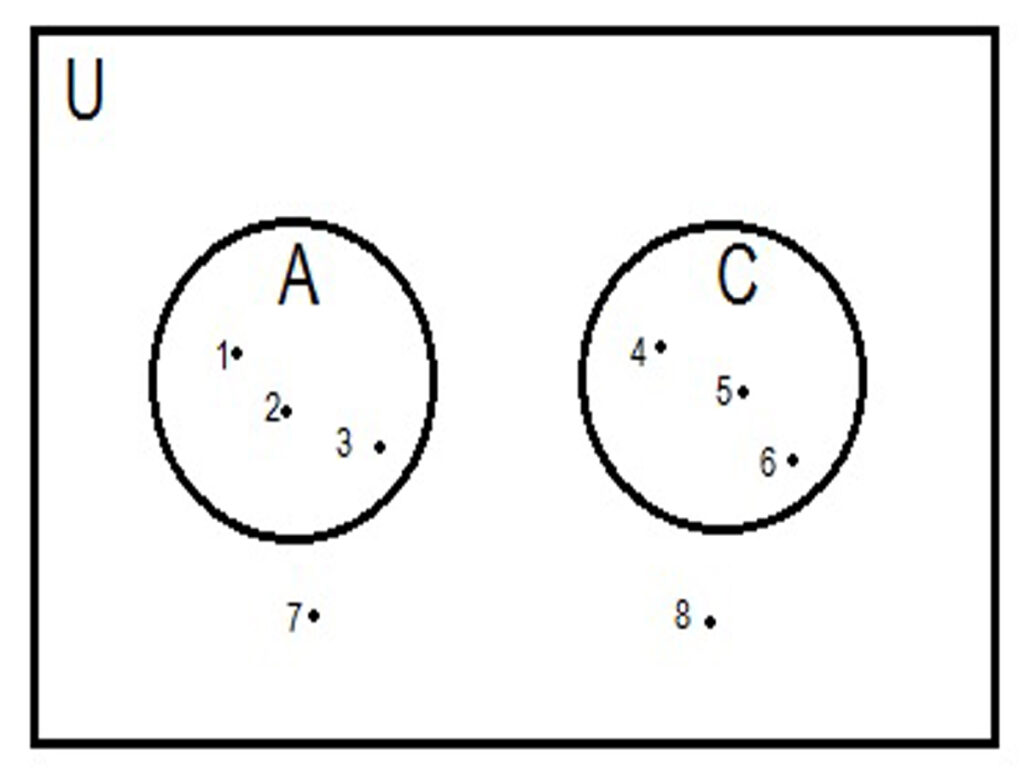
Take sets A = {1,2,3}, B = {2,3,4}, C = {4,5,6}, D = {2,3} and U = {1,2,3,4,5,6,7,8}
These sets can be represented by Venn diagrams as
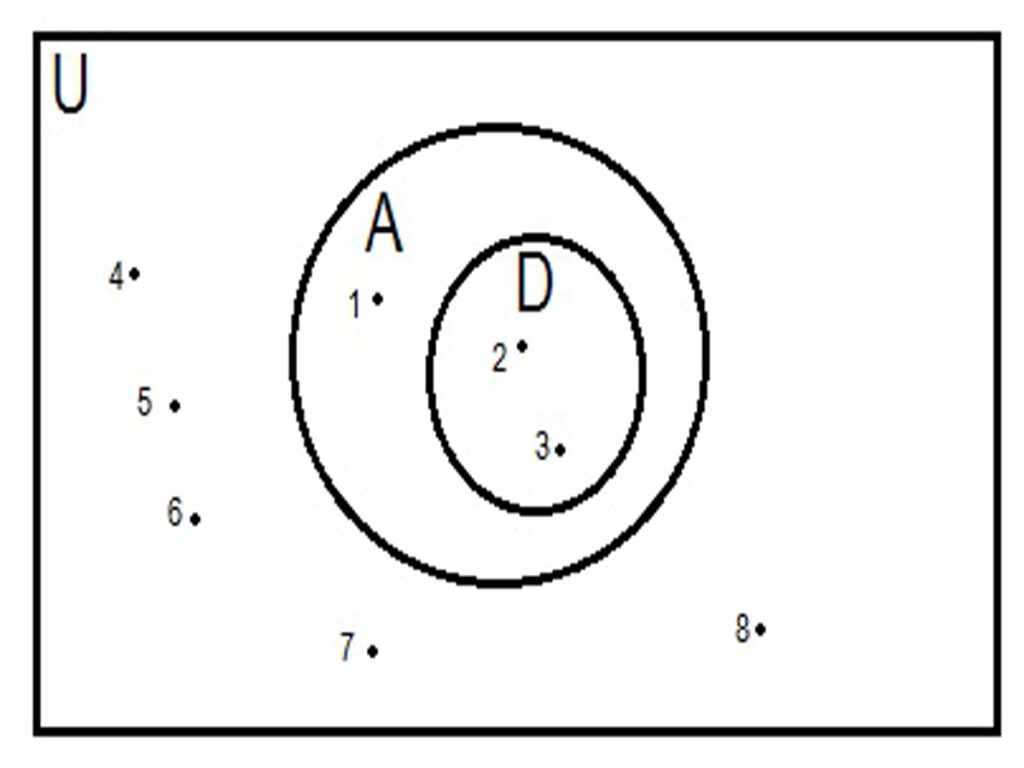
Operation on Sets
Operations on sets:- Just as we perform the operations of addition, subtraction, multiplication and division on numbers. There are certain operations which we can perform on sets. Let us discuss and understand them one by one
1. Union of sets: – The meaning of word union is similar to ‘joining’, ‘uniting’ and ‘mixing’. When we find union of two or more sets we join them together to form a single set containing all the elements of sets being united (denoted by symbol ‘⋃’).
Take sets A = {1,2,3} and B = {2,3,4}
then Union of sets A and B is
A⋃B = {1,2,3,4}
In set builder form AUB = { x:xϵA or xϵB}
Venn diagram for AUB is
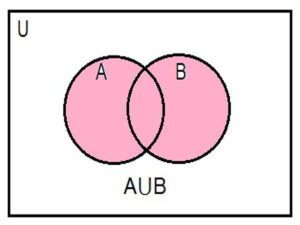
The shaded portion represents AUB
The set A⋃B contains all the elements of set A as well as all the elements of set B including those which are in both set A and set B
2. Intersection of sets: – intersection of two or more sets is a set containing elements which are common in all sets (denoted by symbol’⋂’)
Take sets A = {1,2,3} and B = {2,3,4}
then intersection of sets A and B is
A⋂B = {2,3}
In set builder form A⋂B = x:xϵA and xϵB}
Venn diagram for A⋂B is
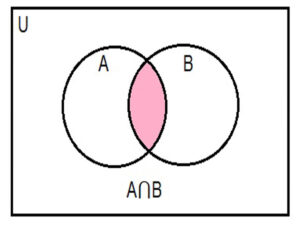
The shaded portion represents A⋂B
3. Difference of two sets:- the difference of two sets A and B denoted by A-B is a set which contains those elements which are in A but not in B
If A = {1,2,3} and B = {2,3,4}
Then A-B = {1}
If we change order then
B-A = {4}
In set builder form
A-B = { x:xϵA and x∉B}
B-A = {x:xϵB and x∉A}
Venn diagram for A-B and B-A are
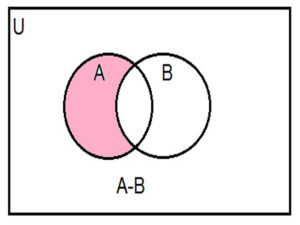
The shaded portion represents A-B
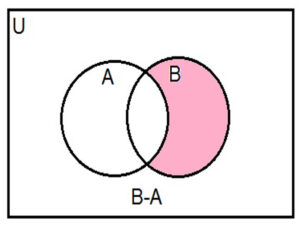
The shaded portion representsB-A
4. Symmetric difference of two sets :- The symmetric difference of two sets A and B (denoted by A∆B) is Union of two sets A – B and B – A
If A = {1, 2, 3} and B = {2, 3, 4}
Then A-B = {1} and B-A = {4}
Then A∆B = (A-B) ⋃ (B-A) = {1,4}
In set builder form
A∆B = {x:xϵA-B or xϵB-A}
Venn diagram for A∆B
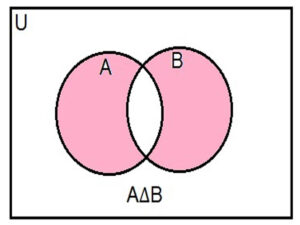
The shaded portion represents A∆B
5. Complement of a set :- Complement of a set is simply difference between universal set and its subset(whose complement we want to find) i.e. U-A where A is subset of U. It is denoted as A’ and
A’ = U-A
So it is clear that a contains all those elements of U which are not in A
If A = {1,2,3} and U = 1,2,3,4,5,6,7,8}
Then A’ = {4,5,6,7,8}
In set builder form
A’ = {x: xϵU and x∉A}
Venn diagram for A’
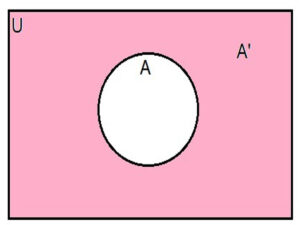
The shaded portion represents A’
Disjoint sets: –Two or more sets having no common element are called disjoint sets, take A = {1,2,3} and C = {4,5,6} clearly no element of A is in C and no element of C is in A i.e. A and C have no common elements hence A and C are disjoints sets.
Also A⋂C = φ
Thus intersection of two disjoint sets is an empty set.
Venn diagram for two disjoint sets is